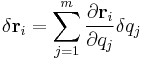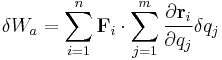Generalized forces

Generalized forces are defined via coordinate transformation of applied forces, 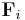$\mathbf{F}_i$ , on a system of n particles, i. The concept finds use in Lagrangian mechanics, where it plays a conjugate role to generalized coordinates.

A convenient equation from which to derive the expression for generalized forces is that of the virtual work, 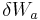$\delta W_a$ , caused by applied forces, as seen in D'Alembert's principle in accelerating systems and the principle of virtual work for applied forces in static systems. The subscript $a$ is used here to indicate that this virtual work only accounts for the applied forces, a distinction which is important in dynamic systems.^[1]^:265

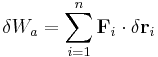
$\delta W_a = \sum_{i=1}^n \mathbf {F}_{i} \cdot \delta \mathbf r_i$

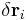$\delta \mathbf r_i$ is the virtual displacement of the system, which does not have to be consistent with the constraints (in this development)

Substitute the definition for the virtual displacement (differential):^[1]^:265

$\delta \mathbf{r}_i = \sum_{j=1}^m \frac {\partial \mathbf {r}_i} {\partial q_j} \delta q_j$

$\delta W_a = \sum_{i=1}^n \mathbf {F}_{i} \cdot \sum_{j=1}^m \frac {\partial \mathbf {r}_i} {\partial q_j} \delta q_j$

Using the distributive property of multiplication over addition and the associative property of addition, we have^[1]^:265

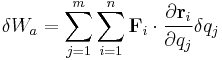$\delta W_a = \sum_{j=1}^m \sum_{i=1}^n \mathbf {F}_{i} \cdot \frac {\partial \mathbf {r}_i} {\partial q_j} \delta q_j$ .

By analogy with the way work is defined in classical mechanics, we define the generalized force as:^[1]^:265

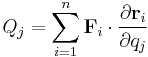$Q_j = \sum_{i=1}^n \mathbf {F}_{i} \cdot \frac {\partial \mathbf {r}_i} {\partial q_j}$ .

Thus, the virtual work due to the applied forces is^[1]^:265

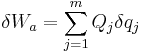$\delta W_a = \sum_{j=1}^m Q_j \delta q_j$ .

References

^ ^a ^b ^c ^d ^e Torby, Bruce (1984). "Energy Methods". Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.

Generalized forces

References

See also